
Transformasi Geometri
A. Pengertian
Transformasi geometri adalah sebuah perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri.
Untuk memindahkan suatu titik atau bangun pada sebuah bidang dapat dikerjakan dengan transformasi.
Apabila hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka dapat disebut transformasi isometri.
B. Jenis - Jenis Transformasi pada Bidang1. Translasi (pergeseran)
2. Refleksi (pencerminan)
3. Rotasi (perputaran)
4. Dilatasi (perkalian)
C. Matriks yang bersesuaian dengan transformasi
1. Translasi (pergeseran)
Translasi (pergeseran) adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan jarak dan arah tertentu.
Jarak dan arah bisa diwakili oleh suatu pasangan biloangan terurut 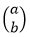
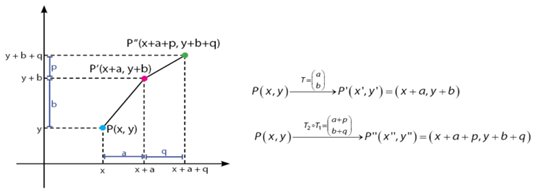
2. Refleksi (Pencerminan)
Merupakan suatu transformasi yang memindahkan suatu titik pada bidang dengan menggunakan sifat bayangan cermin dari titik - titik yang hendak dipindahkan.
Refleksi (pencerminan) diperlukan sebuah garis sebagai sumbu refleksi, garis tersebut merupakan sumbu dari bangun semula dengan bayangannya,
sehingga diperoleh sebagai berikut :
a. Garis yang menghubungkan setiap dengan bayangannya tegak lurus dengan cermin
b. Jarak anatara setiap titik dengan cermin = jarak bayangan ke cermin
c. Bangun dan bayangannya adalah kongruen
1) Rumus Umum Refleksi

2) Jenis - Jenis Pencerminan

3. Rotasi (Perputaran)
Merupakan suatu perubahan kedudukan atau posisi objek dengan cara diputar lewat suatu pusat dan sudut tertentu.
Rotasi ditentukan oleh :
* Titik Pusat rotasi
* Besar sudut rotasi
* Arah rotasi (jika arah rotasi searah jarum jam dikatakan arah negatif, sedangkan berlawanan arah jarum jam dikatakan arah positif)
Adapun rumus yang digunakan dalam rotasi :
· Rotasi sebesar 90° dengan pusat (a,b) : (x,y) → (-y + a+b, x -a + b)
· Rotasi sebesar 180° dengan pusat (a,b) : (x,y) → (-x + 2a+b, -y + 2b)
· Rotasi sebesar -90° dengan pusat (a,b) : (x,y) → (y – b + a, -x + a + b)
· Rotasi sebesar 90° dengan pusat (0,0) : (x,y) → (-y, x)
· Rotasi sebesar 180° dengan pusat (0,0) : (x,y) → (-x, -y)
· Rotasi sebesar -90° dengan pusat (0,0) : (x,y) → (y, -x)
Perlu diketahui bahwa rotasi itu tidak dapat mengubah ukuran :
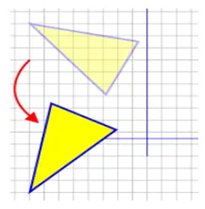
4. Dilatasi
Dilatasi disebut juga dengan perbesaran atau pengecilan suatu objek. Ukuran benda dapat menjadi lebih besar natau lebih kecil.
Perubahan ini bergantung pada skala yang menjadi faktor pengalinya.
Dilatasi dapat ditentukan oleh titik pusat dilatasi dan faktor skala atau faktor dilatasi. Notasi dilatasi dengan titik pusat O (0, 0) dan faktor skala k adalah (O, K)
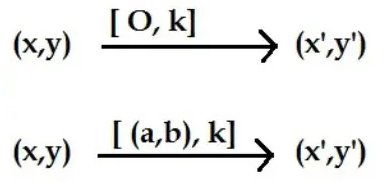
Sifat - Sifat Dilatasi :
- Jika k > 1,maka bangun bayangan diperbesar dan terletak sepihak terhadap pusat dilatasi dan bangun semula.
- Jika 0 < k < 1,maka bangun bayangan diperkecil dan terletak sepihak terhadap pusat dilatasi dan bangun semula.
- Jika -1 < k < 0,maka bangun bayangan diperkecil dan terletak tidak sepihak terhadap pusat dilatasi dan bangun semula.
- Jika k < -1,maka bangun bayangan diperbesar dan terletak tidak sepihak terhadap pusat dilatasi dan bangun semula.












Belum Ada Komentar