Soal - Soal Transformasi Geometri
1. Titik A(5,-2) ditranslasi oleh T (-3, 1). Tentukan koordinat bayangan titik A tersebut!
A. A’(2,1)
B. A’(1,1)
C. A’(2,2)
D. A’(2,-1)
E. A’(-2,1)
Penyelesaian :
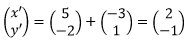
2. Tentukan bayangan garis y = 3x – 5 oleh translasi T (-2, 1)!
A. y = 2x + 2
B. y = 2x – 2
C. y = 3x + 2
D. y = 3x – 2
E. y = 2x + 3
Penyelesaian :
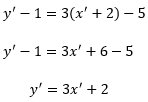
3. Diketahui titik P'(3, - 13) adalah bayangan titik P oleh translasi T = (-10, 7). Koordinat titik P adalah . . .
A. (13, - 20)
B. (13, - 4)
C. (4, 20)
D. (- 5, - 4 )
E. (- 5, - 20)
Penyelesaian :
Misalkan titik (x, y) ditranslasikan oleh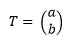 
, sehingga koordinat bayangannya adalah
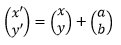
Diketahui : P'(3, - 13) ditranslasikan oleh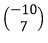 
, sehingga
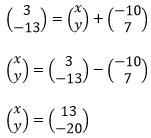
Jadi, koordinat titik P adalah (13, - 20)
4. Bayangan titik P(5, 4) jika didilatasikan terhadap pusat (-2, - 3) dengan faktor skala - 4 adalah . . .
A. ( - 30, - 31)
B. (- 30, 7)
C. (- 26, - 1)
D. ( -14, - 1)
E. ( - 14, - 7)
Penyelesaian :
k = - 4
Misalkan bayangan titik P berada di koordinat ( x', y'), maka
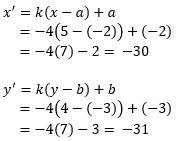
Jadi, koordinat bayangan titik P adalah (- 30, - 31)
5. Tentukan bayangan garis 2x – y = 5 apabila dicerminkan terhadap garis x = -1!
A. 2x + y + 9 = 0
B. x + 2y + 9 = 0
C. x + y - 9 = 0
D. 2x - y + 9 = 0
E. 2x + y - 9 = 0
Penyelesaian :
x = -1
(x, y) --> (2a - x, y)
x' = 2(- 1) - x --> x' = -2 - x
y' = y
2( - 2 - x') - y' = 5
-y - 2x' - y' = 5
2x' + y' + 9 = 0
Jadi, bayangan 2x + y + 9 = 0
6. Tentukan bayangan titik (5, - 3) oleh rotasi R(P, 90) dengan koordinat titik P (- 1, 2) !
A. (8, 4)
B. (-8, 4)
C. (8, - 4)
D. (- 4, - 8)
E. (4, 8)
Penyelesaian :
7. Diketahui koordinat titik P (- 8, 12). Dilatasi (P, 1) memetakan titik (- 4, 8) ke titik . . .
A. (- 4, 8)
B. (- 4, 16)
C. (- 4, - 8)
D. (4, - 16)
E. (4, - 8)
Penyelesaian :
Jika titik (x, y) didilatasikan dengan pusat (a, b) dan faktor skala k, maka bayangan titiknya berada di koordinat (k(x - a) + a, k(y - b) + b).
Bayangan titik (- 4, 8) setelah didilatasikan dengan pusat ( - 8, 12) dan faktor skala 1 adalah
(1 (- 4 - (- 8)) + (- 8), 1(8 - 12) + 12 = (- 4, 8)
Dilatasi (P, 1) memetakan titik ( - 4, 8) ke titik (- 4, 8)
8. Segitiga ABC dengan titik A(- 2, 3), B(2, 3), dan C(0, - 4) didilatasikan dengan pusat O (0,0) dan faktor skala 4. Luas segitiga setelah didilatasikan adalah . . .
A. 120
B. 224
C. 240
D. 280
E. 480
Penyelesaian :
Jika titik (x , y) didilatasikan dengan pusat (0, 0) dan faktor skala k, maka bayangan titiknya berada di koordinat (kx, ky)
Bayangan titik A(- 2, 3) setelah didilatasikan dengan pusat (0, 0) dan faktor skala 4 adalah
A' (4(- 2), 4(3)) = (- 8, 12)
Bayangan titik B(2, 3) setelah didilatasikan dengan pusat (0, 0) dan faktor skala 4 adalah
B' (4(2), 4(3)) = (8, 12)
Bayangan titik C(0, - 4) setelah didilatasikan dengan pusat (0, 0) dan faktor skala 4 adalah
C' (4(0), 4( - 4)) = (0, - 16)
Gambarkan ketiga bayangan titik tersebut dalam sistem koordinat Kartesius, lalu hubungkan sehingga terbentuk segitiga.
Segitiga tersebut memiliki luas :
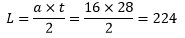
Belum Ada Komentar