
Pertidaksamaan Linear Satu Variabel
Pertidaksamaan linear satu variabel merupakan suatu kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta memuat hubungan (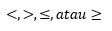 ).
).
Sebagai contohnya, lihat beberapa kalimat seperti di bawah ini :
1. x > 6
2. 3x - 3 < 8
"Masing - masing pertidaksamaan itu hanya mempunyai satu variabel, yaitu x, a dan n. Pertidaksamaan tersebut dinamakan pertidaksamaan satu variabel. Peubah (variabel) pertidaksamaan di atas berpangkat satu atau juga disebut berderajat satu jadi dinamakan pertidaksamaan linear".
Sifat - Sifat Pertidaksamaan Linear Satu Variabel
Seperti yang ada pada A < B pertidaksamaan linear satu variabel x dan C merupakan konstanta tidak nol.
Pertidaksamaan A < B ekuivalen dengan :
1. A + C < B + C
2. A - C < B - C
3.A x C < B x C, bila C > 0 untuk seluruh x
4. A x C > B x C , bila C < 0 untuk seluruh x
5. A/C < B/C, bila C > 0 untuk seluruh x
6. A/C > B/C, bila C < 0 untuk seluruh x
Menyelesaikan Pertidaksamaan Linier Satu Variabel
1. Subtitusi (mengganti)
Menggunakan atau mengganti sembarang x untuk dimasukkan ke dalam formula pertidaksamaan untuk mendapatkan pernyataan yang benar.
Contoh : 5x + 2 > 12
Pembahasan :
Jika x = 1 maka 5 (1) + 2 > 12
5 + 2 > 12
7 > 12 (salah)
Jika x = 3 maka 5 (3) + 2 > 12
15 + 2 > 12
17 > 12 ( pernyataan benar )
2. Ekuivalen
* Menambah dan mengurangi dengan bilangan yang sama, mengalikan atau membagi dengan bilangan positif dan tidak mengubah tanda pertidaksamaan
* Mengalikan atau membagi dengan bilangan negatif dan mengubah tanda pertidaksamaan menjadi lawan misalnya tanda > menjadi <.
Contoh : 2x - 1 > 4x + 5
Pembahasan :
= 2x – 1 + 1 > 4 x + 5 + 1 ( kedua ruas di tambah 1 dan tidak mengubah tanda)
= 2x > 4x + 6
= 2x – 2x > 4x – 2x + 6 (kedua ruas dikurangi 2x)
= -2x > 6
= -2x / -2 > 6/ -2 (kedua ruas dibagi -2 dan mengubah tanda )
= x < -3
Soal Cerita- Tentukan model matematikan dari persamaan panjang kawat yang dibutuhkan dalam x.
- Apabila panjang kawat yang diapakai semuanya tidak lebih dari 132 cm, maka tentukan ukuran dari nilai maksimum dari balok tersebut.
Penyelesaian :
Supaya kita lebih mudah untuk memahami soal di atas, maka perhatikan ilustrasi balok di bawah ini:
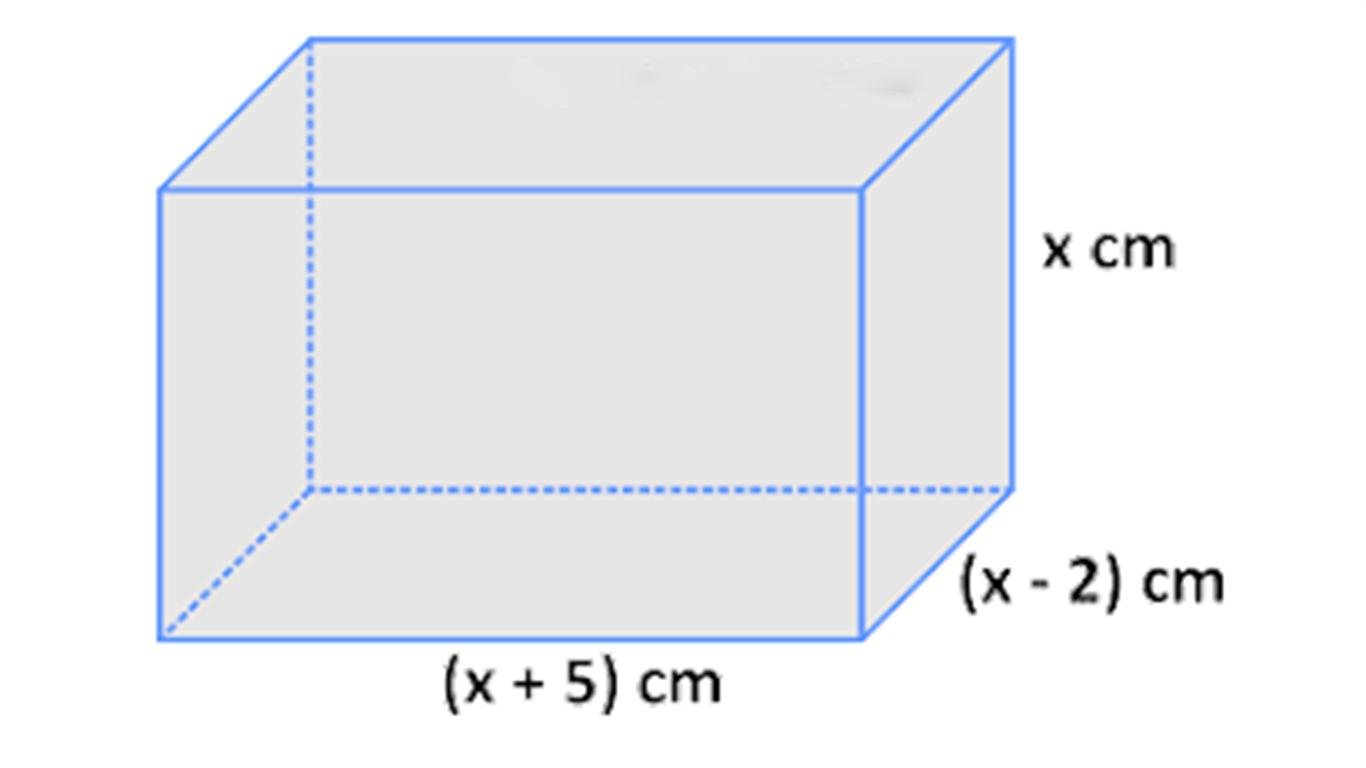
- Menentukan model matematika dari soal di atas.
Contohnya K menyatakan total dari panjang kawat yang diperlukan untuk membuat kerangka balok, maka total panjang kawat yang diperlukan merupakan jumlah dari keseluruhan rusuknya.
Maka, panjang K ialah sebagai berikut.
K = 4p (panjang) + 4l (lebar) + 4t (tinggi)
K = 4(x + 5) + 4(x – 2) + 4x
K = 4x + 20 + 4x – 8 + 4x
K = 12x + 12
Sehingga, kita dapatkan model matematika dari soal cerita nomor dua untuk panjang kawat total yakni K = 12x + 12.
- Menentukan ukuran maksimum balok dari soal di atas.
Panjang kawat tidak boleh melebihi panjang dari 132 cm maka model pertidaksamaannya bisa kita tulis sebagai berikut:
K ≤ 132
12x + 12 ≤ 132
Kemudian kita selesaikan pertidaksamaan linear satu variabel tersebut dengan menggunakan penyelesaian seperti berikuti ini:
12x + 12 ≤ 132
⇒ 12x ≤ 132 – 12
⇒ 12x ≤ 120
⇒ x ≤ 10
Dari penyelesaian x ≤ 10, maka nilai maksimum dari x yaitu 10. Dengan demikian, ukuran balok yakni untuk panjang, lebar dan juga tingginya ialah sebagai berikut:
Panjang = x + 5 ⇔ 10 + 5 = 15 cm
Lebar = x – 2 ⇔ 10 – 2 = 8 cm
Tinggi = x ⇔ 10 cm
Sehingga kita dapatkan maksimum untuk balok tersebut adalah (15 × 8 × 10) cm.












Belum Ada Komentar