
Persamaan Lingkaran
A. Persamaan Lingkaran
Lingkaran adalah tempat kedudukan titik - titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran,
sedangkan jarak titik terhadap pusat lingkaran disebut jari - jari lingkaran.
- Persamaan Umum Lingkaran dapat ditentukan dengan sangat mudah. Perhatikan gambar berikut.
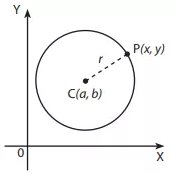
Gambar di atas menunjukkan bahwa terdapat suatu lingkaran yang berpusat di titik C dengan koordinat (a, b) dan berjari - jari r.
Jari - jari merupakan jarak antara titik C dan P. Misalkan titik P (x, y) terletak di keliling lingkaran,
sehingga jarak titik P ke pusat lingkaran dirumuskan sebagai berikut.
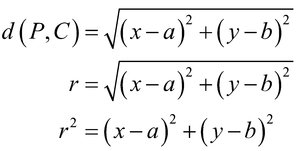
Bentuk Umum Persamaan Lingkaran :
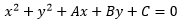
Pusat
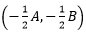
Jari - Jari
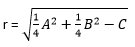
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari - jari r
Jarak dari O (0, 0) ke P (x, y) adalah

Jadi, persamaan lingkaran dengan pusat O (0, 0) dan jari - jari r adalah 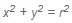
2. Persamaan lingkaran yang berpusat (a,b) dan jari - jari itu r, maka bentuk persamaannya 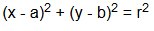
Contoh Soal
1. Jari-jari
dan pusat lingkaran yang memiliki persamaan 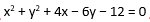 adalah . . .
adalah . . .
A. 5 dan (−2, 3)
B. 5 dan (2, −3)
C. 6 dan (−3, 2)
D. 6 dan (3, −2)
E. 7 dan (4, 3)
Pembahasan :
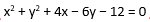
A = 4
B = -6
C = - 12
Pusat :
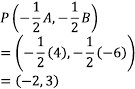
Jari - jari :
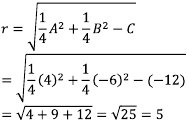
Sehingga jari - jari dan pusatnya adalah 5 dan (-2, 3).
2. Persamaan lingkaran berpusat di mtitik (2, 3) dan melalui titik (5, -1) adalah . . .
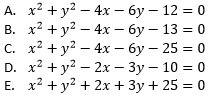
Pembahasan :
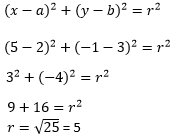
Sehingga :
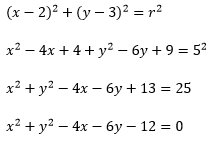












Belum Ada Komentar