
Permutasi
Pengertian
Permutasi dari anggota - anggota himpunan adalah susunan dari semua atau sebagian anggota himpunan itu. Tiap elemen hanya boleh muncul sekali setiap susunan.
Ada tiga contoh permutasi yang sering timbul antara lain: permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, serta permutasi siklis
Macam - Macam Permutasi
1. Permutasi dari n elemen, masing-masing permutasi terdiri atas n elemen
Apabila terdapat unsur yang berbeda dan diambil n unsur, maka banyaknya susunan atau permutasi yang berbeda dari n unsur tersebut merupakan P(n,n) = n! atau nPn = n!
Contoh :
Berapa banyak susunan yang berbeda sanggup dibuat dari huruf-huruf pada kata “MATEMATIKA”
Penyelesaian :
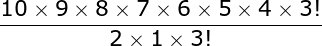
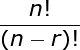
Contoh :
n = 7, r = 4
nPr = n! / (n - r)!
7P4 = 7! / (7 - 4)!
= 7! / 3!
= (7.6.5.4.3!) / 3!
= 7.6.5.4
= 840
Banyaknya susunan ada 840.
Permutasi siklis adalah permutasi yang disusun melingkar. Misalnya A, B, dan C disusun melingkar.
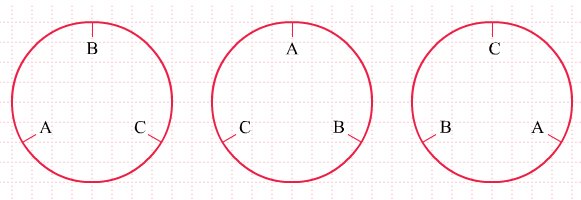
Jika kita pandang urutan itu searah jarum jam maka susunan ABC, CAB, dan BCA adalah sama. Sehingga banyaknya permutasi siklis dari 3 objek adalah 3!/3 = (3 × 2!)/3 = 2! = 2. Jadi, akan dihasilkan 2 susunan yang berbeda secara siklis dari huruf-huruf A, B, dan C, yaitu ABC dan ACB.
Banyaknya permutasi siklis dari n objek dapat dinyatakan dengan (n – 1)!
Dalam sebuah keluarga yang terdiri dari seorang ayah, seorang ibu, dan 3 orang anaknya makan bersama dan mengelilingi sebuah meja makan. Berapa banyaknya cara yang berlainan saat mereka dapat duduk, jika: mereka berpindah-pindah tempat.
Penyelesaian :
Banyaknya anggota keluarga adalah 5 orang (seorang ayah, seorang ibu,
dan 3 orang anak). Sehingga, banyaknya cara yang berlainan saat mereka
duduk berpindah-pindah tempat adalah (5 – 1)! = 4! = 24 cara












Belum Ada Komentar