
Pengertian Selang dan Penyelesaian Pertidaksamaan Linear
1. Pengertian Selang
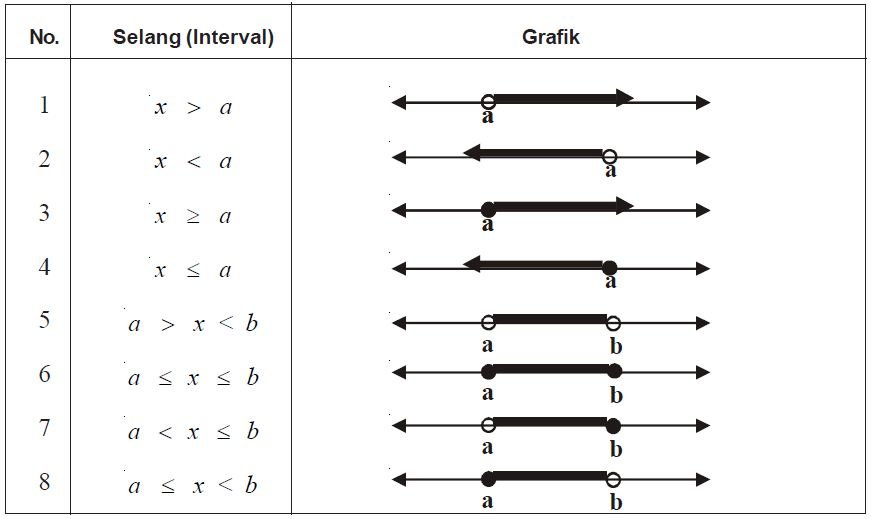
Selang atau interval dapat dinyatakan dalam garis bilangan dan himpunan. Untuk menentukan batas - batas interval pada garis bilangan digunakan tanda berikut.
a. Tanda  jika bilangan pada tanda ini masuk ke dalam interval.
jika bilangan pada tanda ini masuk ke dalam interval.
b. Tanda  jika bilangan pada tanda ini tidak masuk ke dalam interval.
jika bilangan pada tanda ini tidak masuk ke dalam interval.
Bagian garis yang menyatakan selang digambar dengan garis yang lebih tebal atau dengan memberi arsiran di atas garis tersebut.
Berikut adalah berbagai bentuk selang yang dinyatakan dalam garis bilangan dan himpunan.
2. Penyelesaian Pertidaksamaan Linear
Pertidaksamaan linear adalah suatu pertidaksamaan yang memuat peubah - peubah yang berpangkat satu.
Contoh :
a. 3x - 1 > 0, merupakan pertidaksamaan linear dengan satu peubah, yaitu x.
b. 2x + 5y < 3, merupakan pertidaksamaan linear dengan dua peubah, yaitu x dan y.
c. x + 2y - z 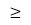 1, merupakan pertidaksamaan linear dengan tiga peubah, yaitu x, y, dan z.
1, merupakan pertidaksamaan linear dengan tiga peubah, yaitu x, y, dan z.
Untuk selanjutnya yang akan kita pelajari hanyalah pertidaksamaan linear dengan satu peubah.
Menyelesaikan pertidaksamaan linear berarti menentukan nilai peubah yang memenuhi pertidaksamaan tersebut dengan cara menyederhanakan bentuk pertidaksamaan. Berikut sifat - sifat pertidaksamaan yang digunakan untuk menyederhanakan pertidaksamaan.
a. Suatu pertidaksamaan jika kedua ruasnya ditambah atau dikurangi dengan bilangan yang sama, diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula.
b. Suatu pertidaksamaan jika kedua ruasnya dikalikan dengan suatu bilangan positif yang sama, diperoleh pertidaksamaan baru yang ekuivalen dengan pertidaksamaan semula.
c. Suatu pertidaksamaan jika kedua ruasnya dikalikan dengan suatu bilangan negatif yang sama, diperoleh pertidaksamaan baru. Pertidaksamaan baru itu ekuivalen dengan pertidaksamaan semula jika arah dari tanda pertidaksamaan itu dibalik.
Penyelesaian dari pertidaksamaan berupa interval atau selang bilangan nyata yang dapat digambarkan pada garis bilangan.












Belum Ada Komentar