
Pengertian Jenis-jenis dan Transpose Matriks
Pengertian Matriks
Matriks adalah susunan bilangan atau elemen-elemen yang disusun dalam baris dan kolom sehingga membentuk persegi. Bilangan pada matriks disebut elemen/unsur matriks. Baris pada matriks merupakan susunan bilangan secara mendatar (horizontal). Sedangkan kolom pada matriks adalah susunan bilangan secara tegak (vertikal).
Ordo atau Ukuran Matriks
Ukuran matriks atau biasa yang disebut ordo ditentukan dari banyaknya baris dan kolom yang tersusun pada suatu matriks. Jika matriks A tersusun dari banyaknya i baris dan j kolom maka dapat dituliskan dengan Aij atau matriks A berukuran ixj.
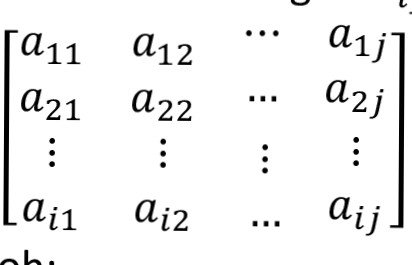
Contoh:
Diketahui matriks M sebagai berikut.
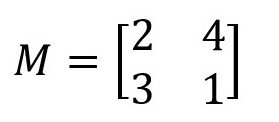
Matriks M berordo 2x2. Karena terdapat sebanyak 2 baris dan 2 kolom.
Jenis-jenis Matriks
- Matriks nol
Matriks yang elemen penyusunnya adalah nol.
Contoh:
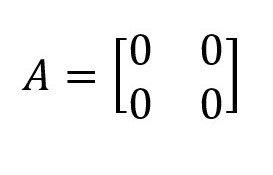
- Matriks baris
Matriks yang ordonya hanya memiliki 1 baris saja.
Contoh:
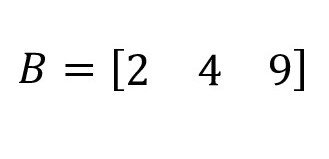
- Matriks kolom
Matriks yang ordonya hanya memiliki 1 kolom saja.
Contoh:
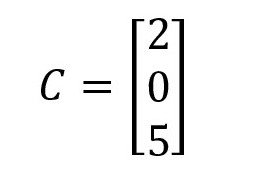
- Matriks persegi
Matriks yang ordonya sebanyak . Atau banyaknya baris dan kolom adalah sama.
Contoh:
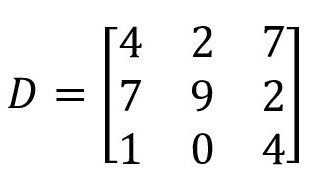
- Matriks diagonal
Matriks persegi yang elemen diagonalnya bilangan selain nol dan bagian atas dan bawah diagonalnya adalah angka nol.
Contoh:
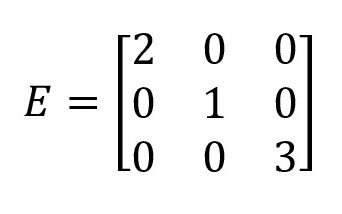
- Matriks segitiga atas
Matriks persegi yang semua elemen dibawah diagonal utamanya adalah angka nol.
Contoh:
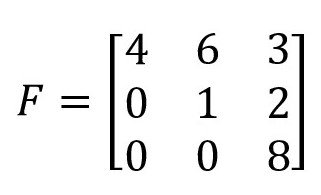
- Matriks segitiga bawah
Matriks persegi yang semua elemen diatas diagonal utamanya adalah angka nol.
Contoh:
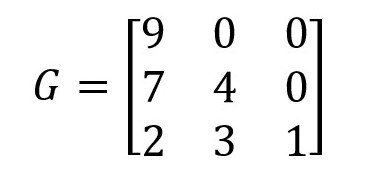
- Matriks identitas
Matriks persegi yang diagonal utamanya adalah angka 1 dan sisanya angka nol.
Contoh:
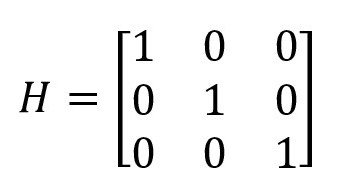
Transpose Matriks
Transpose matriks adalah matriks baru yang diperoleh dengan mengubah baris menjadi kolom dan kolom menjadi baris dari elemen matriks sebelumnya. Penulisan transpose pada matriks dinotasikan dengan huruf T kecil dibagian atas. Transpose matriks yang dilakukan pada matriks persegi akan menghasilkan ordo matriks baru yang sama (jika ordo 3x3 maka akan tetap 3x3). Namun, jika transpose dilakukan pada matriks selain persegi maka akan mengubah dan menukar ukuran baris dan kolomnya. Misal, transpose yang dilakukan pada matriks 2x3 maka akan mendapatkan matriks baru dengan ordo 3x2.
Contoh:
Ubahlah matriks berikut kedalam bentuk transpose!
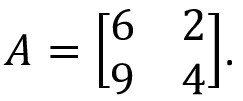
Pembahasan:
Karena diubah menjadi transpose, maka elemen baris menjadi kolom dan elemen kolom menjadi baris. Sehingga didapatkan:
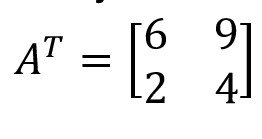











Belum Ada Komentar