les privat | bimbel Semarang | TK/SD/SMP/SMA/UMUM/STAN

Latihan - Latihan Soal Dimensi Tiga

Mapel Sabtu, 14 Desember 2019

1. Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H ke garis AC adalah . . . cm

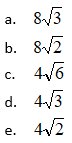
Pembahasan :

Jarak titik H ke garis AC adalah OH.
rusuk = a = 8
OH = $\frac{a/}{2}$ √6 = $\frac{8/}{2}$ √6 = 4√6
Jawaban : C

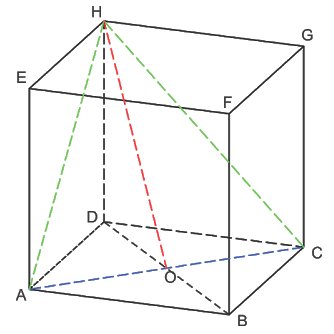
2.Panjang rusuk kubus $A B C D . E F G H$ adalah $12 cm$ . Jika $P$ titik tengah $C G$ , maka jarak titik $P$ ke garis $H B$ adalah $\dots \cdot$
A. $8 \sqrt{5} cm$ D. $6 \sqrt{2} cm$
B. $6 \sqrt{5} cm$ E. $6 cm$
C. $6 \sqrt{3} cm$

$Penyelesaian :$

* DB merupakan diagonal bidang pada kubus, maka panjang
$DB = \sqrt(AD² + AB²) = \sqrt(12² + 12²) = 12\sqrt2 cm$

$*$ BH merupakan diagonal ruang pada kubus, maka panjang
BH = √(DH² + DB²)
$= \sqrt(12² + (12\sqrt2)²) = 12\sqrt3 cm$

* karena P titik tengah CG, maka
HP = √(HG² + GP²)

= √(12² + 6²) = 6√5 cm

* jarak dari P ke H sama dengan jarak dari P ke B, maka ∆PBH adalah segitiga samakaki sehingga jarak P ke garis BH adalah tinggi segitiga ∆PBH

t = PV = √(PH² + VH²)
= √((6√5)² + (6√3)²

= 6√2 cm

Jadi jarak P ke garis BH adalah 6√2 cm

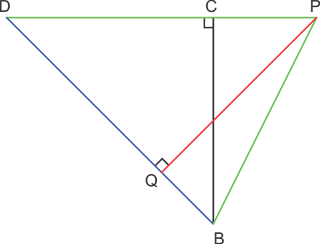
3. Diketahui kubus ABCD.EFGH, panjang rusuk kubus adalah 12 cm. Titik P terletak pada perpanjangan rusuk DC sehingga CP : DP = 1 : 3. Jarak titik P dengan bidang BDHF adalah ...
A. 6√2 cm
B. 9√2 cm
C. 12√2 cm
D. 16√2 cm
E. 18√2 cm

Penyelesaian :

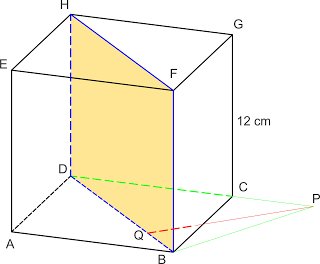
Jarak titik P ke bidang BDHF = jarak titik P ke garis BD ⇒ PQ.
rusuk = a = 12
CP : DP = 1 : 3 ⇒ DC : CP = 2 : 1
DC = 12 ⇒ CP = 6
DP = DC + CP = 12 + 6 =18
BD = a√2 = 12√2

Perhatikan segitiga BDP

Dengan menggunakan rumus luas segitiga diperoleh :
$\frac{1/2}{}$ × BD × PQ = $\frac{1/2}{}$ × DP × BC
BD × PQ = DP × BC
12√2 × PQ = 18 × 12
⇒ PQ = 9√2

4. Diketahui kubus $A B C D . E F G H$ dengan panjang rusuk $8$ cm. Panjang proyeksi $D E$ pada $B D H F$ adalah $\dots \cdot$
A. $2 \sqrt{2} cm$ D. $4 \sqrt{6} cm$
B. $2 \sqrt{6} cm$ E. $8 \sqrt{2} cm$
C. $4 \sqrt{2} cm$

$Penyelesaian :$

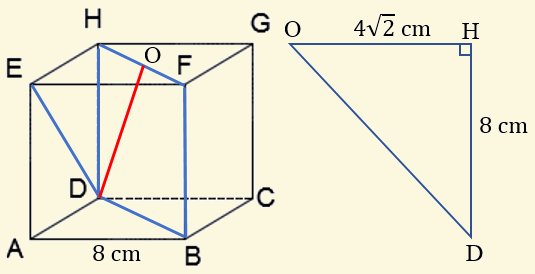
Panjang proyeksi = OD

OD² = ED² - EO²
= (8√2)² - (4√2)²
= 128 - 32
= 96
OD = √96
= 4√6

5.

Diketahui panjang rusuk kubus di atas adalah 10 cm. Titik P dan titik Q berturut-turut merupakan titik tengah dari rusuk AB dan BC. Jarak garis PQ ke garis EG adalah ….

$[ textrm{A.} ; ; ; frac{2}{5} sqrt{6} ; textrm{cm}]$

$[ textrm{B.} ; ; ; frac{3}{5} sqrt{6} ; textrm{cm}]$

$[ textrm{C.} ; ; ; frac{4}{5} sqrt{6} ; textrm{cm}]$

$[ textrm{D.} ; ; ; frac{3}{2} sqrt{6} ; textrm{cm}]$

$[ textrm{E.} ; ; ; frac{5}{2} sqrt{6} ; textrm{cm}]$

Penyelesaian :

Perhatikan garis PQ dan garis EG!

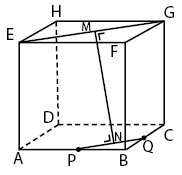
Berdasarkan teorema Phytagoras, maka dapat diperoleh panjang PQ dengan cara berikut.

$[ PQ = sqrt{BP^{2} + BQ^{2}} ]$

$[ PQ = sqrt{5^{2} + 5^{2}} ]$

Mencari panjang QN:

$[ QN = frac{1}{2} PQ]$

$[ QN = frac{1}{2} cdot 5sqrt{2}]$

$[ QN = frac{5}{2} sqrt{2} ; textrm{cm} ]$

Mencari panjang BN:

Berdasarkan teorema pythagoras (segitiga siku-siku di N), sehingga

$[ BN = sqrt{BQ^{2} - QN^{2}}]$

$[ BN = sqrt{5^{2} - left( frac{5}{2} sqrt{2} right)^{2}}]$

$[ BN = sqrt{25 - frac{25}{4} cdot 2} ]$

$[ BN = sqrt{frac{100}{4} - frac{50}{4}} ]$

$[ BN = sqrt{frac{50}{4}} ]$

$[ BN = frac{sqrt{50}}{sqrt{4}} ]$

$[ BN = frac{sqrt{25 cdot 2}}{2} ]$

$[ BN = frac{sqrt{25} cdot sqrt{2}}{2} ]$

$[ BN = frac{5 sqrt{2}}{2} ]$

$[ BN = frac{5}{2} sqrt{2} ; textrm{cm} ]$

Mencari panjang FM:

FM merupakan setengah panjang diagonal sisi kubus (sisi EG), sehingga panjangnya adalah

$[FM = frac{1}{2} cdot 10sqrt{2} = 5 sqrt{2} ; textrm{cm} ]$

Ingat!!!

Panjang diagonal sisi kubus adalah $textrm{sisi} sqrt{2}$ .

Panjang diagonal ruang kubus adalah $textrm{sisi} sqrt{3}$ .

Selanjutnya perhatikan gambar berikut!

Soal dan Pembahasan soal mencari jarak antara dua jarak

Mencari panjang MF’:

$[ MF' = 5 sqrt{2} - frac{5}{2} sqrt{2} ]$

$[ MF' = frac{10}{2} sqrt{2} - frac{5}{2} sqrt{2} ]$

$[ MF' = frac{5}{2} sqrt{2} ; textrm{cm} ]$

Mencari Panjang MN:

$[MN = sqrt{textrm{MF'}^{2} + textrm{NF'}^{2}} ]$

$[MN = sqrt{left( frac{5}{2} sqrt{2} right) ^{2} + 10^{2}} ]$

$[MN = sqrt{ frac{25}{4} cdot {2} + 100} ]$

$[MN = sqrt{ frac{50}{4} + frac{400}{4}} ]$

$[MN = sqrt{ frac{450}{4}} ]$

$[MN = frac{sqrt{450}}{sqrt{4}} ]$

$[MN = frac{sqrt{225 cdot 2}}{2} ]$

$[MN = frac{{sqrt{225} cdot sqrt{2}}}{2} ]$

$[MN = frac{{15sqrt{2}}}{2} ]$

$[MN = frac{15}{2}sqrt{6} ; textrm{cm} ]$

Jadi panjang garis MN dengan garis EG adalah $frac{15}{2} sqrt{2}$ cm.

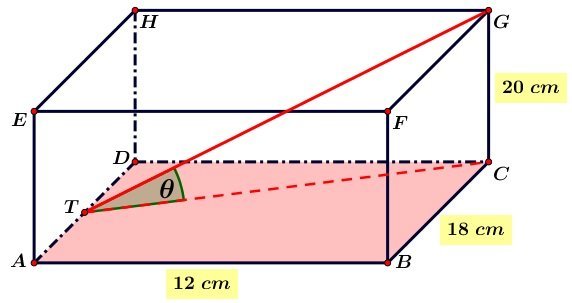
6. Diketahui balok $A B C D . E F G H$ dengan $A B = 12 c m$ dan $B C = 18 c m$ dan $C G = 20 c m$ . $T$ adalah titik tengah $A D$ . Jika $θ$ adalah sudut antara garis $G T$ dengan bidang $A B C D$ , maka nilai $c o s θ$ adalah...
$\begin{matrix} \end{matrix}$

Penyelesaian :

Jika kita gambarkan Balok $A B C D . E F G H$ , titik $T$ dan sudut $θ$

seperti berikut ini:

\begin{matrix} \end{matrix}

$\begin{matrix} \end{matrix}$

Latihan - Latihan Soal Dimensi Tiga

Bagikan Post

Komentar

Belum Ada Komentar

Tambahkan Komentar

Profil

Kategori

Berita Terbaru

Video

Event Terdekat

Testimonial

Latihan - Latihan Soal Dimensi Tiga

Bagikan Post

Komentar

Belum Ada Komentar

Tambahkan Komentar

Profil

Subscribe

Kategori

Berita Terbaru

Video

Event Terdekat

Testimonial