Fungsi
Fungsi dari himpunan A ke himpunan B adalah pengawanan setiap unsur A ke tepat satu unsur B.
Dikatakan suatu fungsi jika :
a. Setiap anggota A mempunyai kawan di B.
b. Kawan setiap anggota A di himpunan B adalah tunggal.
Fungsi f yang mengawankan anggota himpunan A dengan anggota himpunan B dapat digambarkan sebagai berikut.
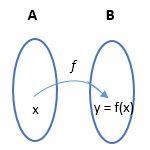
a. A disebut daerah asal (domain) fungsi f
b. B disebut daerah kawan (kodomain) fungsi f
c. Himpunan semua anggota B yang mempunyai kawan di A disebut daerah hasil (range)
a. Fungsi Onto (Surjektif)
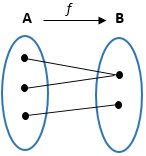Fungsi f : A --> B disebut onto, jika setiap anggota B mempunyai pasangan anggota A.
b. Fungsi Satu - satu (Injektif)
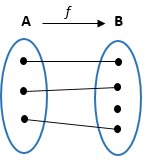
Fungsi f : A --> B disebut satu - satu jika untuk anggota B yang mempunyai pasangan dengan anggota A,
pasangan tersebut hanya satu.
c. Fungsi Korespondensi Satu - Satu (Bijektif)
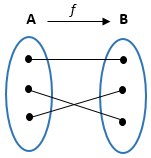
Fungsi f : A --> B disebut korespondensi satu - satu jika fungsi tersebut surjektif sekaligus injektif.
Grafik Fungsi Aljabar Sederhana
Fungsi aljabar adalah fungsi yang melibatkan bentuk aljabar dan operasinya. Adapun beberapa fungsi aljabar sederhana beserta grafiknya.
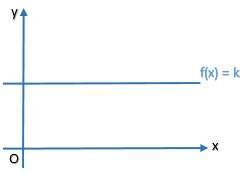
a. Fungsi konstan adalah fungsi yang mengawankan setiap anggota domain dengan suatu kostanta. Fungsi konstan dituliskan
f : x --> k sehingga rumusnya f(x) = k dengan k suatu konstanta. Grafik fungsi konstan berupa garis mendatar.
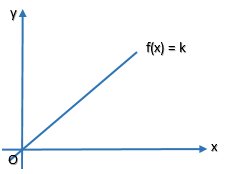
b. Fungsi Identitas
Fungsi identitas adalah fungsi yang mengawankan setiap anggota domain dengan dirinya sendiri. Grafik fungsi identitas berupa
garis miring.
c. Fungsi Linear
Bentuk umum fungsi linear adalah f(x) = ax + b, dengan a dan b bilangan riil serta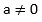 
. Grafik fungsi linear f(x) = ax + b berupa
garis yang selalu melalui titik (0, b) dan (-b/a, 0).
d. Fungsi Kuadrat
Grafik fungsi kuadrat f(x) = ax2 + bx + c berupa parabola.
1. Diketahui fungsi f : x --> 2x + 1 dari himpunan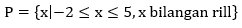 
ke himpunan bilangan rill.
a. Tentukan nilai fungsi f untuk x = - 2, x = 0, x = 2, dan x = 5!
b. Tentukan domain, kodomain, dan range dari fungsi tersebut!
Penyelesaian :
Fungsi f : --> 2x + 1, maka rumus fungsinya f(x) = 2x + 1.
a. Nilai fungsi f :
Untuk x = -2 adalah f (-2) = 2(-2) + 1 = -3
Untuk x = 0 adalah f(0) = 2(0) + 1 = 1
Untuk x = 2 adalah f(2) = 2(2) + 1 = 5
Untuk x = 5 adalah f(5) = 2(5) + 1 = 11
b. Domain =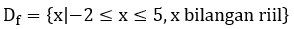 
Kodomain =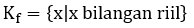 
Range = Rf
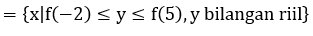
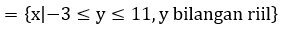
2. Didefinisikan fungsi f(x) =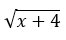 
. Tentukan nilai f(5) !
Penyelesaian :
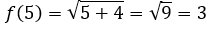
3. Diberikan himpunan A = {1, 2, 3} dan B = {a, b, c}. Jika f : A --> B dengan f = {(1, c), (2, a), (3,c)}, apakah f merupakan fungsi ?
Jika f merupakan fungsi, tentukan sifat - sifatnya !
Penyelesaian :
Setiap anggota domain (A) tepat mempunyai satu kawan di kodomain (B) sehingga f merupakan fungsi.
Fungsi f bukan fungsi surjektif karena ada anggota B yang tidak mempunyai pasangan dengan anggota A.
Fungsi f bukan fungsi injektif karena ada anggota B yang mempunyai 2 kawan di A.
Jadi, fungsi f tidak surjektif dan tidak injektif.
Belum Ada Komentar